波数ベクトル

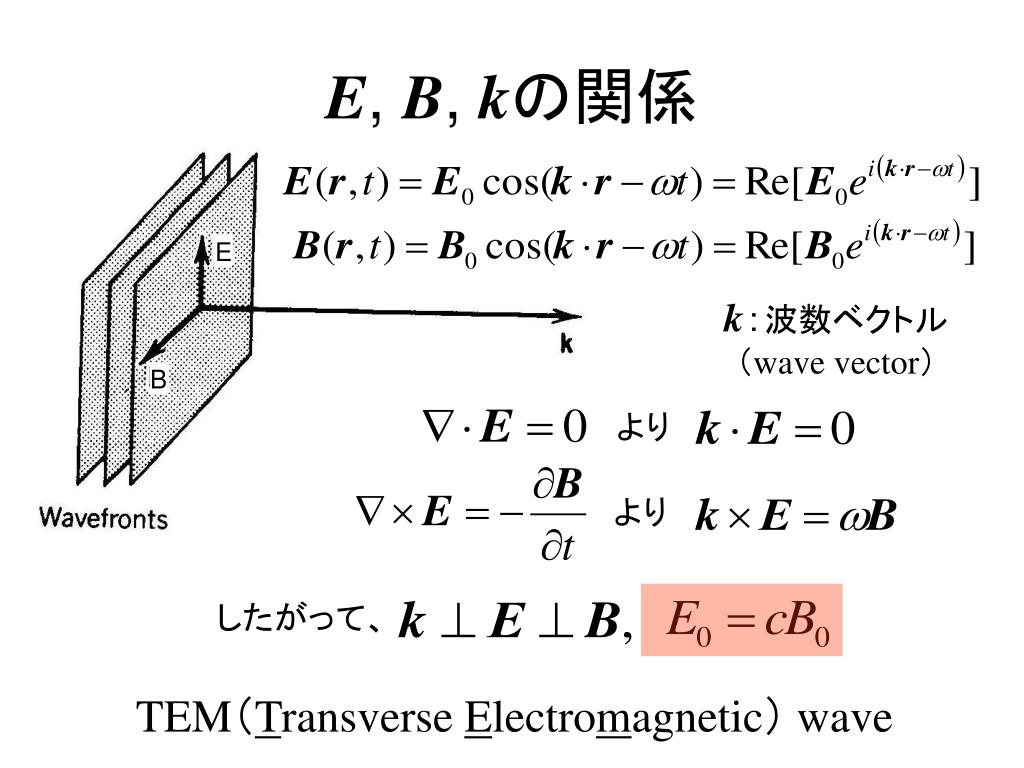
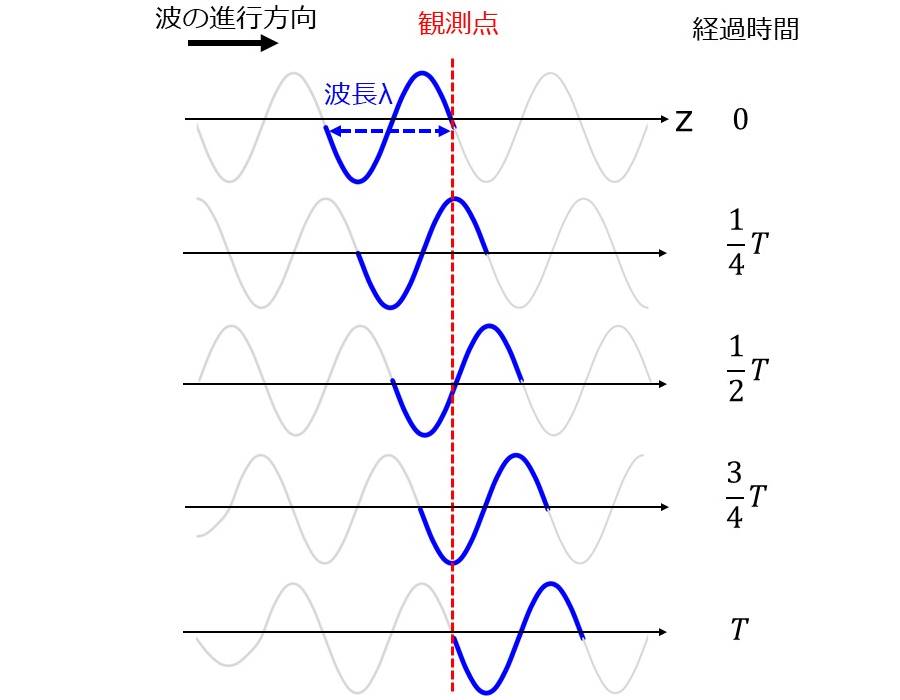
物理学における波数ベクトルとは、波動を記述するのに用いられるベクトルである。全てのベクトルのように大きさと方向を持ち、これら両方が重要である。その大きさは波の波数または角波数であり、波長に反比例する。その方向は通常、波動の伝播の方向であるが、いつもそうとは限らない（以下を参照）。

特殊相対論の文脈では、波数ベクトルは4元ベクトルとしても定義できる。

定義

波数ベクトルには2つの一般的な定義があり、大きさが因子2πだけ異なる。 1つ目の定義は物理学などで用いられ、もう一つの定義は結晶学などで用いられる。この記事ではそれらを「物理学の定義」と「結晶学の定義」とそれぞれ呼ぶ。

物理学の定義

理想的な1次元の進行波は次の方程式に従う。

\psi (x,t)=A\cos(kx-\omega t \varphi )

ここで、

xは位置。
tは時間。
$\psi$ (xとtの関数)は波を記述する攪乱（たとえば海洋波における $\psi$ は水の高さであり、音波における $\psi$ は空気圧である）。
Aは波の振幅。
$\varphi$ は「位相角」で、2つの波がお互いにどれだけ同期していないかを記述する。
$\omega$ は波の時間的な角周波数で、単位時間あたりどれだけ沢山の振動が完了するかを記述する。周期 $T$ と方程式 $\omega =2\pi /T$ によって関連している。
$k$ は波の空間的な角周波数（波数）であり、単位空間あたりどれだけ沢山の振動が完了するかを記述する。波長と式 $k=2\pi /\lambda$ によって関連している。

この波動は xの方向に速度（より正確には位相速度） $\omega /k$ で進行する。

結晶学の定義

結晶学において、同じ波動はわずかに異なる方程式を用いて記述される。 1次元と3次元ではそれぞれ、

\psi (x,t)=A\cos(2\pi (kx-\nu t) \varphi )

\psi \left({\mathbf {r} },t\right)=A\cos \left(2\pi ({\mathbf {k} }\cdot {\mathbf {r} }-\nu t) \varphi \right)

違いは、

角周波数 $\omega$ の代わりに周波数 $\nu$ が用いられる。これらは $2\pi \nu =\omega$ の関係にある。この記事においてこの置き換えは重要ではないが、結晶学の一般的慣習を反映している。
波数kと波数ベクトルkは異なる方法で定義される。上述の物理学の定義では $k=|{\mathbf {k} }|=2\pi /\lambda$ であるが、一方ここでは $k=|{\mathbf {k} }|=1/\lambda$ である。

kの方向は以下で議論する。

波数ベクトルの方向

波数ベクトルが指す方向は「波動の伝播の方向」とは区別しなければならない。「波動の伝播の方向」は波動のエネルギー流れの方向であり、小さな波束が動く方向、つまり群速度の方向である。光波では、これはポインティングベクトルの方向でもある。一方で波数ベクトルは位相速度の方向を指す。言い換えれば波数ベクトルは、定位相の面（波面とも呼ばれる）の法線方向を指す。

無損失等方性媒質(空気や全ての気体、ガラスのようないくつかの固体など)において、波数ベクトルの方向は波動の伝播の方向と全く同じである。媒質の損失が大きい場合、一般的に波数ベクトルは波動の伝播の方向以外の方向を指す。波数ベクトルが波動が伝播する方向と同じである条件は、波動が均一であることであり、媒質の損失が大きいときは必ずしもそうとは限らない。均一な波動において定位相の面は、一定振幅の面でもある。不均一な波動では、これら2つの種類の面は方向が異なる。波数ベクトルは常に一定位相の面と垂直である。

例えば、非対称結晶中の光波や堆積岩中の音波のように、波動が異方性媒質中を進行するとき、波数ベクトルは波動伝播の方向を必ずしも指すわけではない。

固体物理学

固体物理学において、結晶中の電子や正孔の「波数ベクトル」（k-ベクトルとも呼ばれる）は、その量子力学的な波動関数の波数ベクトルである。それらの電子波は、通常のサイン波ではなく、サイン波である一種の「包絡関数」を持ち、波数ベクトルは通常「物理学の定義」を用いてその包絡波を用いて定義される。詳細はブロッホ波を参照。