複素数の偏角

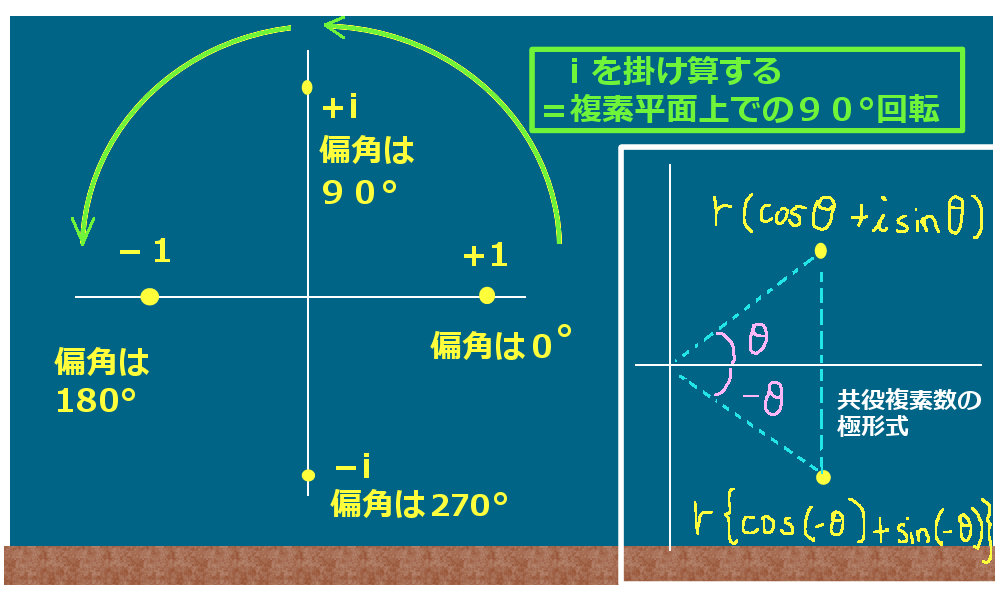
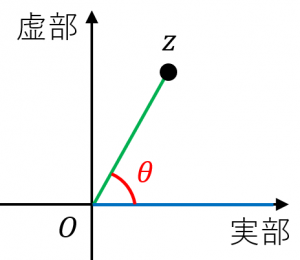
数学において、複素数の偏角（へんかく、英: argument of complex）とは、複素数平面上で複素数が表す点の動径が表す一般角のことである。複素数 z の偏角は記号で arg z で表す。偏角はラジアンで表す。

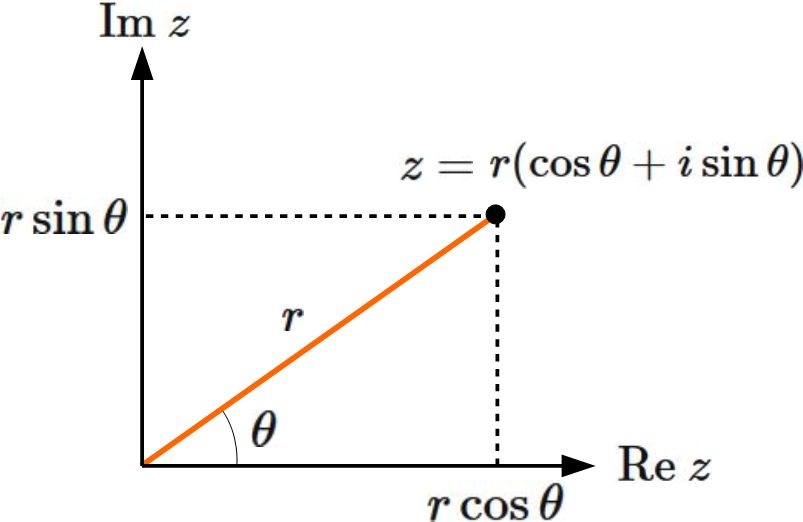
複素数を極形式表示することで、絶対値と偏角が得られる。これにより、複素数の乗除が簡明に行うことができる。

複素数に対する偏角は、2π の任意の整数倍を足す分だけ表し方がある。つまり、多価関数である。そこで表示を一意にするには、主値を決め、区間 (−π, π] などに制限する。

2π の任意の整数倍の差を除いて次の等式が成り立つ：

arg zw ≡ arg z arg w

arg z/w ≡ arg z − arg w

(何れも mod 2π)

定義

複素数 z = x yi の偏角は、arg z と書かれ、正の実軸から動径 Oz までの角度を反時計回りに測った角度である。弧度法で表示する。時計回りに測ると負になる。

複素数に対する偏角の表示を一意にするために、主値を区間 (−π, π] に制限する。[0, 2π) にすることもある。

主値を (−π, π] にすると、逆正接関数 tan⁻¹ を用いて次のように表せる：

${\displaystyle \arg z={\begin{cases}\tan ^{-1}{\dfrac {y}{x}}&(x>0)\\[0.1em]\tan ^{-1}{\dfrac {y}{x}} \pi &(x<0\,\land \,y\geqq 0)\\[0.1em]\tan ^{-1}{\dfrac {y}{x}}-\pi &(x<0\,\land \,y<0)\\[0.1em]{\dfrac {\pi }{2}}&(x=0\,\land \,y>0)\\[0.1em]-{\dfrac {\pi }{2}}&(x=0\,\land \,y<0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}}$

上記の式には条件分岐が多数あるが、符号関数 sgn やヘヴィサイドの階段関数 H(x) を用いることで次のようにまとめることもできる：

${\displaystyle {\begin{aligned}\arg z&={\begin{cases}\tan ^{-1}{\dfrac {y}{x}} {\dfrac {1-\operatorname {sgn} x}{2}}(1 \operatorname {sgn} y-|\operatorname {sgn} y|)\pi &(x\neq 0)\\[0.1em](\operatorname {sgn} y){\dfrac {\pi }{2}}&(x=0\,\land \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\\&={\begin{cases}\tan ^{-1}{\dfrac {y}{x}} \{1-H(x)\}\{2H_{1}(y)-1\}\pi &(x\neq 0)\\[0.1em](\operatorname {sgn} y){\dfrac {\pi }{2}}&(x=0\,\land \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\end{aligned}}}$

0 × (0 除算を含む式) = 0 と形式的に考えることで、更にまとめることもできる：

${\displaystyle {\begin{aligned}\arg z&={\begin{cases}|\operatorname {sgn} x|\tan ^{-1}{\dfrac {y}{x}} {\dfrac {1-\operatorname {sgn} x}{2}}(1 \operatorname {sgn} y-|\operatorname {sgn} y|)\pi &(x\neq 0\,\lor \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\\&={\begin{cases}|\operatorname {sgn} x|\tan ^{-1}{\dfrac {y}{x}} \{1-H_{1/2}(x)\}\{2H_{1}(y)-1\}\pi &(x\neq 0\,\lor \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\end{aligned}}}$

あるいは、逆余弦関数 cos⁻¹ や逆正弦関数 sin⁻¹ を用いて次のように表すこともできる：

${\displaystyle {\begin{aligned}\arg z&={\begin{cases}(1 \operatorname {sgn} y-|\operatorname {sgn} y|)\cos ^{-1}{\dfrac {x}{|z|}}&(x\neq 0\,\lor \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\\&={\begin{cases}\{2H_{1}(y)-1\}\cos ^{-1}{\dfrac {x}{|z|}}&(x\neq 0\,\lor \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\end{aligned}}}$

${\displaystyle {\begin{aligned}\arg z&={\begin{cases}(1 \operatorname {sgn} x-|\operatorname {sgn} x|)\sin ^{-1}{\dfrac {y}{|z|}} {\dfrac {|\operatorname {sgn} x|-\operatorname {sgn} x}{2}}(1 \operatorname {sgn} y-|\operatorname {sgn} y|)\pi &(x\neq 0\,\lor \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\\&={\begin{cases}\{2H_{1}(x)-1\}\sin ^{-1}{\dfrac {y}{|z|}} \{1-H_{1}(x)\}\{2H_{1}(y)-1\}\pi &(x\neq 0\,\lor \,y\neq 0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}\end{aligned}}}$

ここで、|z| は複素数の絶対値で、|z| = √x² y² である。

主値を [0, 2π) にするには、上記の定義で、負となる偏角の値に対しては 2π を加えることにすればよい。

偏角を「位相」、振幅と呼んだりすることもある。

基本的な性質

• ${\displaystyle |z|\cos(\arg z)=\operatorname {Re} z}$
• ${\displaystyle |z|\sin(\arg z)=\operatorname {Im} z}$
• ${\displaystyle \arg {\bar {z}}=-\arg z}$
• ${\displaystyle \arg 0}$ は不定

主値をとる偏角

主値 (−π, π] における偏角の値を、記号で Arg z（最初の文字を大文字）で表すことがある。表記には揺れがあり、arg と Arg が文献によって逆になることもあることに注意。

${\displaystyle \arg z=\{\operatorname {Arg} z 2\pi n\mid n\in \mathbb {Z} \}}$

${\displaystyle \operatorname {Arg} z=\{\arg z-2\pi n\mid n\in \mathbb {Z} \,\land \,(-\pi <\operatorname {Arg} z\leqq \pi )\}}$

数値計算

複素数 z = x yi の偏角は逆正接関数 arctan y/x で表せる。

x > 0 のとき、すなわち −π/2 < Arg z < π/2 のとき

Arg z = tan⁻¹ y/x

が成り立つが、x > 0 以外の場合の偏角を逆正接関数で表すには、場合分けが必要である。x < 0 の場合はさらに y > 0 と y < 0 の場合に分ける。

${\displaystyle \operatorname {Arg} (x iy)={\begin{cases}\tan ^{-1}{\dfrac {y}{x}}&(x>0)\\[0.2em]\tan ^{-1}{\dfrac {y}{x}} \pi &(x<0\,\land \,y\geqq 0)\\[0.1em]\tan ^{-1}{\dfrac {y}{x}}-\pi &(x<0\,\land \,y<0)\\[0.1em]{\dfrac {\pi }{2}}&(x=0\,\land \,y>0)\\[0.1em]-{\dfrac {\pi }{2}}&(x=0\,\land \,y<0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}}$

上半平面、下半平面ごとに表示することもできる：

${\displaystyle \operatorname {Arg} (x iy)={\begin{cases}{\dfrac {\pi }{2}}-\tan ^{-1}{\dfrac {x}{y}}&(y>0)\\[0.1em]-{\dfrac {\pi }{2}}-\tan ^{-1}{\dfrac {x}{y}}&(y<0)\\[0.1em]0&(x>0\,\land \,y=0)\\[0.1em]\pi &(x<0\,\land \,y=0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}}$

Arg の主値を区間 [0, 2π) とする変種では、値が負のときに値に 2π を足すことで得られる。

正接の半角公式 tan θ/2 = sin θ/1 cos θ を用いると、1つの計算式で表せる：

${\displaystyle \operatorname {Arg} (x iy)={\begin{cases}2\tan ^{-1}{\dfrac {y}{{\sqrt {x^{2} y^{2}}} x}}&(x>0\,\lor \,y\neq 0)\\[0.1em]\pi &(x<0\,\land \,y=0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}}$

ただし、この表示は、計算の精度が上記より下がる。

この表示は、x < 0, y = 0 の近くでは 不定形 0/0 に近づき、浮動小数点の計算において、計算が不安定となり、オーバーフローする可能性がある。この範囲でのオーバーフローを避けるには、もう1つの正接の半角公式 tan θ/2 = 1 − cos θ/sin θ を用いて次の計算式が使われる：

${\displaystyle \operatorname {Arg} (x iy)={\begin{cases}2\tan ^{-1}{\dfrac {{\sqrt {x^{2} y^{2}}}-x}{y}}&(y\neq 0)\\[0.1em]0&(x>0\,\land \,y=0)\\[0.1em]\pi &(x<0\,\land \,y=0)\\[0.1em]{\text{indeterminate}}&(x=y=0)\end{cases}}}$

主値 Arg は、プログラミング言語の数学ライブラリでは関数 atan2 あるいはその変種の言語を用いて多くの通常利用可能である。atan2(y, x) の主値は区間 (−π, π] である。

積・商の偏角

2つの複素数の乗除は、極形式表示することにより、簡明に行うことができる。複素数 z₁, z₂ の極形式表示を

z₁ = r₁(cos φ₁ i sin φ₁)

z₂ = r₂(cos φ₂ i sin φ₂)

とすると、

arg z₁z₂ ≡ arg z₁ arg z₂

arg z₁/z₂ ≡ arg z₁ − arg z₂

(何れも mod 2π)

z ≠ 0 で n が整数のとき、

arg zⁿ ≡ n arg z　(mod 2π)

例

${\displaystyle {\begin{aligned}\arg(2 i) \arg(3 i)&=\arg(2 i)(3 i)\\&=\arg(5 5i)\\&={\dfrac {\pi }{4}}{\pmod {2\pi }}\quad //\end{aligned}}}$

脚注

文献

外部リンク

• Weisstein, Eric W. "Complex Argument". mathworld.wolfram.com (英語).